Modéliser les actions mécaniques usuelles
Notation
Dans toute cette partie, \(\vec{u}\) est un vecteur unitaire, son sens et son orientation sont définis sur chaque schéma.
Recenser les actions mécaniques : graphe d'analyse ou graphe de structure
Définition :
Un graphe d'analyse ou graphe de structure est un graphe des liaisons complété des actions mécaniques sollicitant le mécanisme étudié. Il permet de recenser efficacement toutes les actions mécaniques.
Exemple :
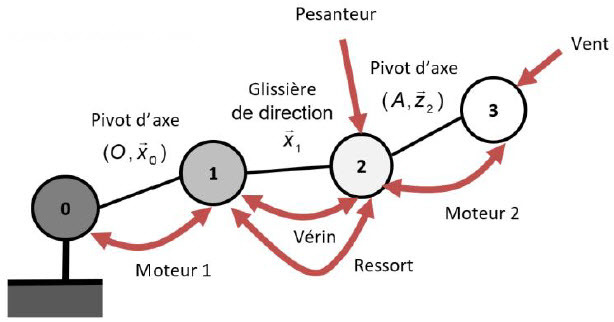
Action mécanique de pesanteur (poids)
Définition :
Le poids d'un solide 1 de masse m est une force de résultante \(m. \vec{g}\) passant par le centre de masse G : \(\left \{F_{pes \to 1} \right \} = \left \{ \begin{matrix} m. \vec{g} \\ \overrightarrow{0} \end{matrix}\right \}_{\forall M \in (G, \vec{g})}\)
Remarque :
Écrit en un autre point de la droite d'action \((G, \vec{g})\), le torseur de l'action mécanique de pesanteur a son moment non nul.
Action mécanique d'entraînement d'un vérin
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
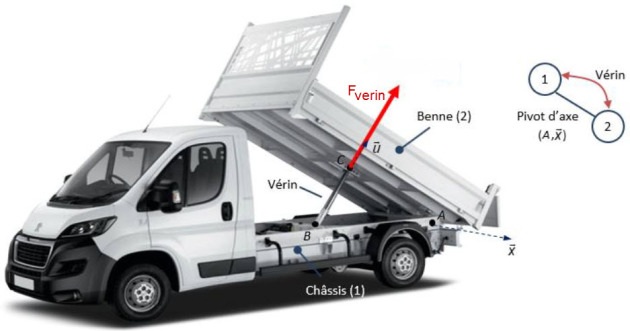
Si pour un vérin :
le corps et la tige sont en liaison articulation (pivot ou sphérique) à leur « point d'attache B et C » ;
et que les poids du corps et de la tige sont négligés,
alors l'action mécanique du vérin est modélisée par une force de droite d'action passant par ses points d'attache : \(\left \{F_{verin \to 2} \right \} = - \left \{F_{verin \to 1} \right \} = \left \{ \begin{matrix} F_{verin}. \vec{u} \\ \vec{0} \end{matrix}\right \}_{\forall P \in (BC)}\)
Remarque : le corps et la tige du vérin ne sont pas représentés sur le graphe d'analyse, alors qu'ils sont représentés sur la photo afin de connaître la droite d'action.
Complément :
Si en plus le vérin est de type pneumatique ou hydraulique et en considérant que la pression du fluide est uniforme :
\(\left \{F_{verin \to 2} \right \} = - \left \{F_{verin \to 1} \right \} = \left \{ \begin{matrix} p.S. \vec{u} \\ \vec{0} \end{matrix}\right \}_{\forall P \in (BC)}\) avec :
p : la pression du fluide (en Pa)
S la surface de contact fluide/piston (en m²) :
Si la tige sort : \(S=\dfrac{\pi . D^2}{4}\)
Si la tige rentre : \(S=\dfrac{\pi . (D^2 - d^2)}{4}\)
Remarque :
Unités de pression usuelles :
un Pascal ( Pa ) est égal à un Newton par mètre carré, \(1 Pa = 1 N.m^{-2}\) ;
un Méga Pascal (MPa) est égal à 1 Newton par millimètre carré,\( 1 MPa = 10^6 Pa = 1 N.mm^{-2}\) ;
le bar ( bar ) ,\( 1 bar = 10^5 Pa\)
Action mécanique d'entraînement d'un moteur électrique
Considérons le rotor et le stator d'un moteur :
L'action mécanique du stator (1) d'un moteur électrique sur son rotor (2) est modélisée par un couple orienté par l'axe du moteur : \(\left \{F_{moteur \to 2} \right \} = - \left \{F_{moteur\to 1} \right \} = \left \{ \begin{matrix}\vec{0} \\ C_{mot} . \vec{u} \end{matrix}\right \}_{\forall P}\)
Remarque : le rotor (2) est en liaison pivot par rapport au stator (1).
Action mécanique d'un ressort de traction/compression
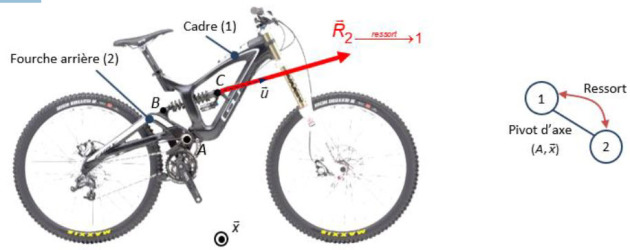
Considérons deux solides 1 et 2 en liaison pivot. Un ressort de traction/compression est placé en parallèle de cette liaison. Soit \(\lambda\) la longueur du ressort.
L'action mécanique d'un ressort de traction/compression de longueur à vide \(\lambda_0\) et de raideur \(k\) (en N/m) est une force passant par ses points d'attache et d'intensité proportionnelle à la variation de longueur du ressort :\( \left \{F_{ressort \to 1} \right \} = - \left \{F_{ressort \to 2} \right \} = \left \{ \begin{matrix} -k.(\lambda - \lambda_0).\vec{u} \\ \vec{0} \end{matrix}\right \}_{\forall P \in (BC)}\)
Remarque : écrit en un autre point de la droite d'action (AB) , le torseur de l'action possède un moment.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Action mécanique d'un ressort de torsion
Considérons deux solides 1 et 2 en liaison pivot. Un ressort de torsion est placé en parallèle de cette liaison. Soit \(\alpha\) l'angle du ressort.
L'action mécanique d'un ressort de torsion d'angle à vide \(\alpha_0\) et de raideur \(k\) (en Nm/rad) est un couple, d'intensité proportionnelle à la variation de l'angle du ressort : \(\left \{F_{ressort \to lisse} \right \} = - \left \{F_{ressort \to bati} \right \} = \left \{ \begin{matrix} \vec{0} \\ -k.(\alpha- \alpha_0).\vec{u} \end{matrix}\right \}_{\forall P}\)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
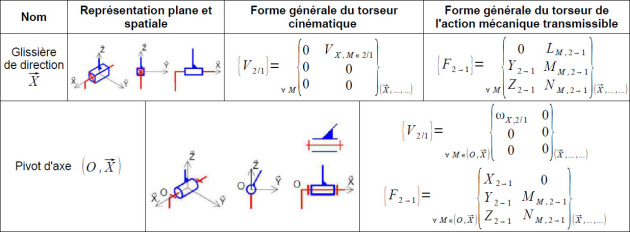
Actions mécaniques transmissibles d'un solide à l'autre dans une liaison pivot ou glissière parfaites.
Fondamental :
Une liaison pivot ou glissière entre deux solides indéformables permet de contrôler les mouvements relatifs entre ces deux solides mais aussi de transmettre des efforts.
Dans une liaison parfaite, l'action transmise par la liaison ne s'oppose pas au(x) mouvement(s) possible(s).
Exemple :
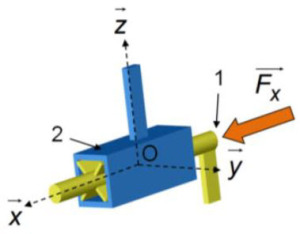
Soit une liaison glissière de direction \(\vec{x}\) entre 1 et 2.
La liaison comprend 1 degré de liberté : \(T_x\) .
Si on applique une force \(\vec{F_x}\) sur le solide 1, le solide 2 ne « ressent » rien, car la force n'est pas transmise du solide 1 au solide 2 par l'intermédiaire de la liaison.
Conséquence : la liaison ne peut pas transmettre d'action élémentaire suivant \(\vec{x}\) , d'où \(X_{1 \to 2}=0\)
Texte légal :
Les composantes non nulles de \(\overrightarrow{F_{ 2 \to 1}}\) et \(\overrightarrow{M_{M, 2 \to 1}}\) sont appelées inconnues de liaisons. En général, dans les problèmes rencontrés, elles sont inconnues et on ne cherche pas forcement à les déterminer...