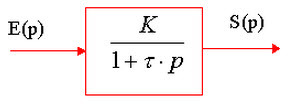1er ordre
Définition :
Un système physique d'entrée \(e(t)\) et de sortie \(s(t)\) est du 1er ordre, si il est régi par une équation différentielle du 1er ordre à coefficients constants du type : \(\tau . \frac{d s(t)}{dt} + s(t) = K.e(t)\)où
\(K\) est le gain statique du système (unité :\(\left( \dfrac {unite \ de \ s(t)}{unite \ de \ e(t)} \right)\)) e,
\( \tau \) est la constante de temps (en\(\left( s \right)\) ),
Si les conditions initiales sont nulles (\(s(0)=0\)), la fonction de transfert dans le domaine de Laplace s'écrit : \(H(p)= \frac{S(p)}{E(p)} = \frac{K}{1+ \tau .p}\)
qui peut se présenter sous la forme :